Face clearance between gear tooth? Backlash? Torsional Backlash? Angular Minute? The Key to Planetary Gearbox Precision

To put it simply, the precision of a planetary gearbox usually refers to the degree of accuracy and uniformity of the motion produced by the final actuating element, due to the input from the power source during the transmission process.

The discussion below is based on the impact of gears on precision, but in reality, the machining errors, geometric errors, and assembly quality of each of the matching parts of the gearbox are also important factors that affect the precision of the gearbox.

 

I. Terminology Explanation:

A. Torsional backlash jt [arcmin]: Term

Refers to the maximum deviation angle between the output shaft of the gearbox and the input end. During measurement, the gear input end is fixed first, and then a certain torque is applied to the output shaft to overcome the friction and oil film resistance inside the gearbox. Typically, 2-3% of the rated torque is used. At this point, there is a slight displacement at the output end of the gearbox, and this angular displacement is known as torsional backlash, measured in 'arc minutes', which is one-sixtieth of a degree.

 

B. Angular minute [arcmin]: Unit of measurement (a sexagesimal unit of angle) also known as "minute of angle"

As it is based on the sexagesimal system, the unit relationship is as follows: 1° (degree) = 60' (minutes of angle) = 3600" (seconds of angle). A circle has 360 degrees, and one degree can be divided into 60 angular minutes, meaning a circle has 21,600 angular minutes. If the torsional backlash is marked as 1 arcmin, it means that for one complete rotation of the gearbox, there is an angular deviation of 1/60 degree.

In practical applications, this angular deviation is related to the shaft diameter and the size of the turntable.

For example: When the radius of the output end turntable is 300mm, and the precision of the gearbox is jt=3 (arcmin), the deviation per revolution of the gearbox is b=0.26mm. Please refer to the calculation formula in "II. Explanation: A."

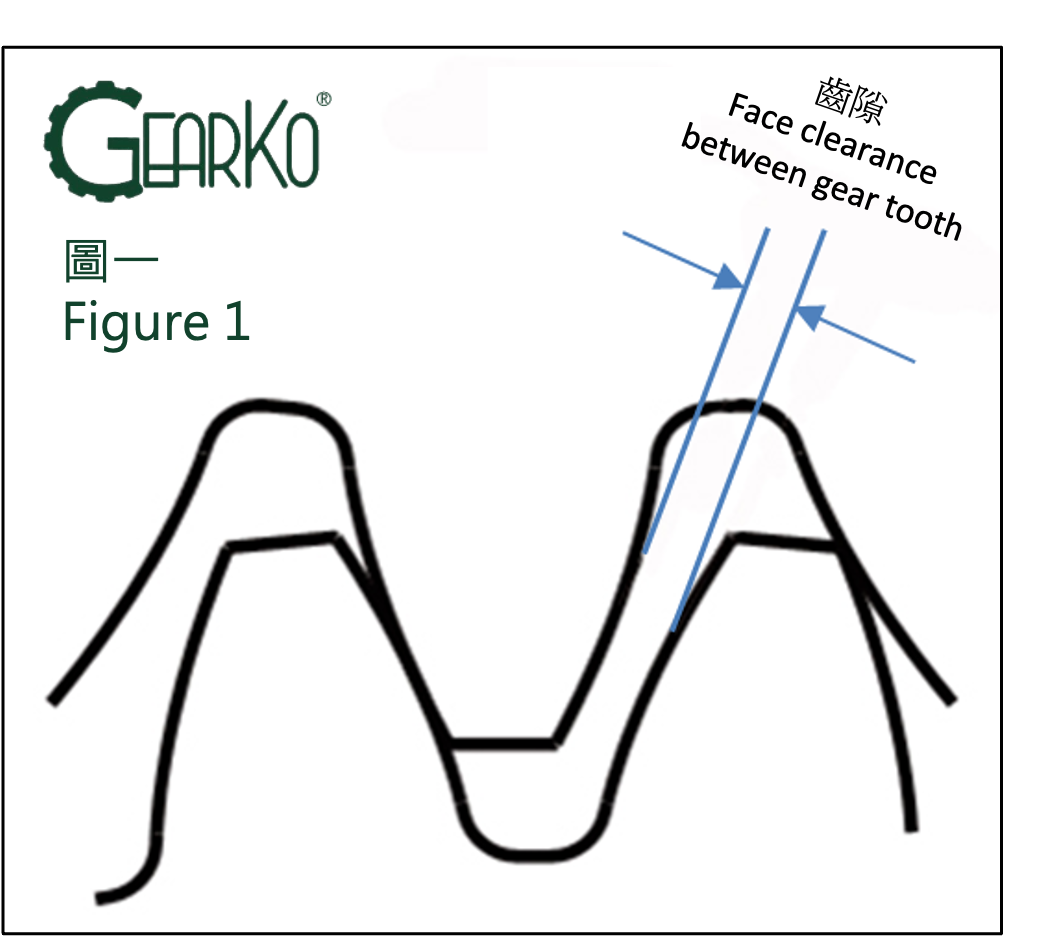
C. Face clearance between gear tooth: Term

Here, we discuss the most intuitive normal directional clearance, which refers to the shortest distance on the non-meshing tooth face when one side of two gears' meshing surfaces is in contact, as shown in the figure below.

In addition to normal directional clearance, there is also circumferential directional tooth clearance, rotational angle tooth clearance, and radial tooth clearance. Clearances caused by tolerances in these dimensions can also affect overall precision.

 

II. Explanation:

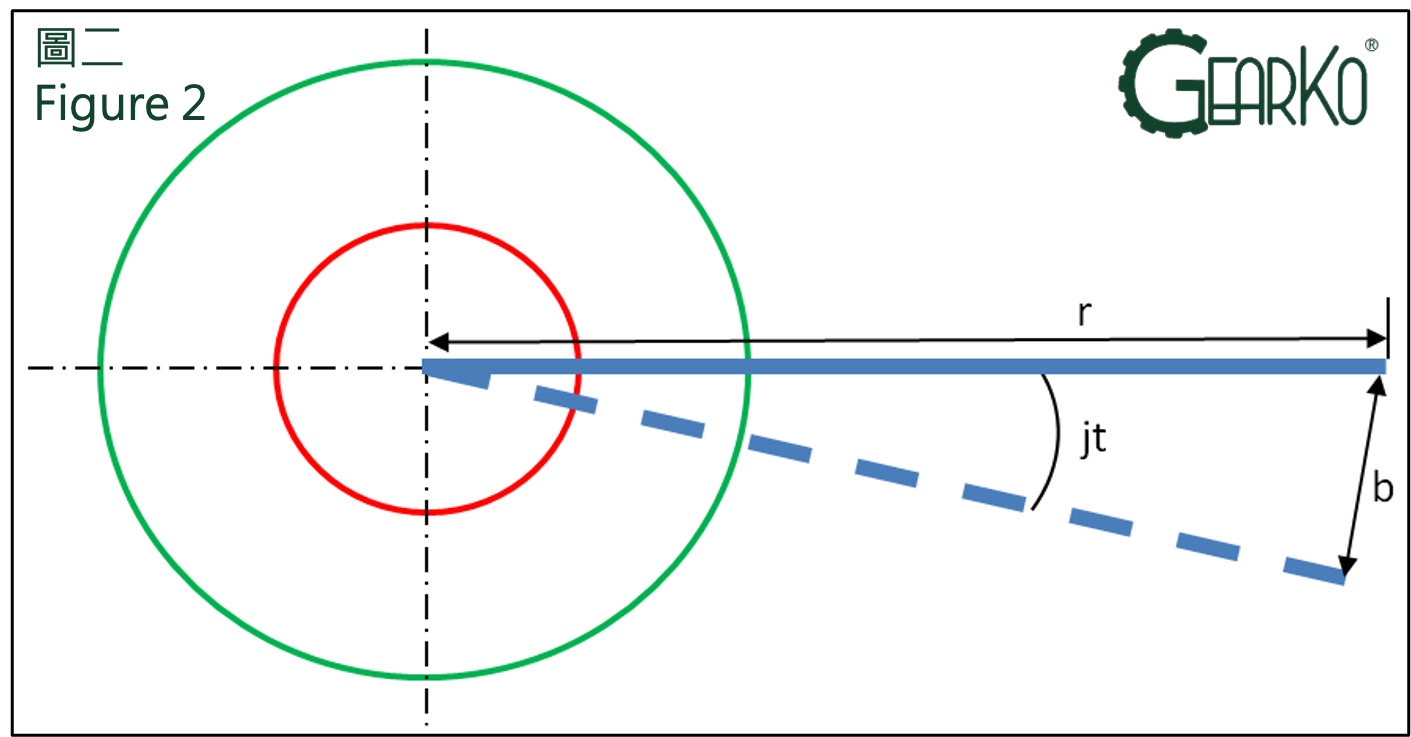
A. Torsional Backlash (in angular minutes):

Let's explain the concept of torsional backlash using the idea of manual measurement, which is essentially converting arc length into an angle. When using manual measurement, the input end is first fixed, and then a longer lever arm is installed on the output end. A dial (or digital) indicator is used to measure the amount of displacement over a certain distance (note 1), and the corresponding rotational angle is calculated, which is the torsional backlash (in angular minutes), as shown in the Figure below.

Example:

Angular minute formula: jt=bx21600/(2･π･r), where radius r=300mm, and arc length b=0.26

Angular minute jt=0.26 x21600/(2･π･300)≒3 arcmin

B. Backlash and Face Clearance: The size of the face clearance directly affects the torsional backlash because when gears rotate, the movement is a combination of rolling and sliding between the tooth surfaces. If there is no clearance between the gears, they would interfere with each other and not be able to rotate, so face clearance is a necessary design aspect of gear transmission.

If the gears rotate only in one direction, the gears will maintain contact and the face clearance will not cause an issue. However, in reciprocating motion, the clearance leads to a situation where, when the motor completes the input action and stops, the final positioning point will not be reached immediately. Instead, due to the clearance, the gears will rotate slightly in the reverse direction before making contact and transmitting the power.

From a microscopic perspective, this small segment of clearance causes the power source to idle, meaning that the input angle cannot be fully transferred to the final position. If the clearance is too large, precision decreases; if it's too small, it can affect the smoothness of operation. Therefore, this balance increases the difficulty and cost of manufacturing planetary gearboxes.

 

III. Application:

A. Rotational Motion:

For example: When the output end turntable has a radius of 500mm, and the precision of the gearbox is 3 arcmin, the deviation at the outermost edge of the disc is 0.44mm.

 

B. Linear Motion:

For example: With a ball screw having a lead of 20mm, and the precision of the gearbox is 3 arcmin, the linear deviation is 20/21600*3=0.00278mm.

 

The two application methods mentioned above clearly show the deviations caused by gearbox precision in different applications. Whether these deviations are within an acceptable range requires further understanding of the user's needs.

 

IV. Conclusion:

When someone asks about the face clearance, backlash, torsional backlash, or angular minutes, it's akin to asking:

 

"How much does this dumbbell weigh?" or "What is the weight of this dumbbell in kilograms?"

"How long is this fishing rod?" or "How many feet is this fishing rod?"

In essence, it is just a different colloquial way of speaking, and industry professionals usually understand what is being asked.

They want to know the precision of the gearbox in angular minutes.

 

As mentioned at the beginning, there are many factors that affect the precision of planetary gearboxes, and there will always be some deviation between practical measurements and theoretical values, especially in multi-stage gearboxes. This is due to the impact of clearance at each stage, and the fact that the clearances at each meshing point are not the same. Combined with various other errors, all these can affect the overall precision of gear rotation.

GearKo gearboxes are known for their excellent precision, rigidity, and high reliability, offering a cost-performance ratio that is competitive with any quality brand. If there are any needs or questions, you are welcome to call or email GearKo for contact.

 

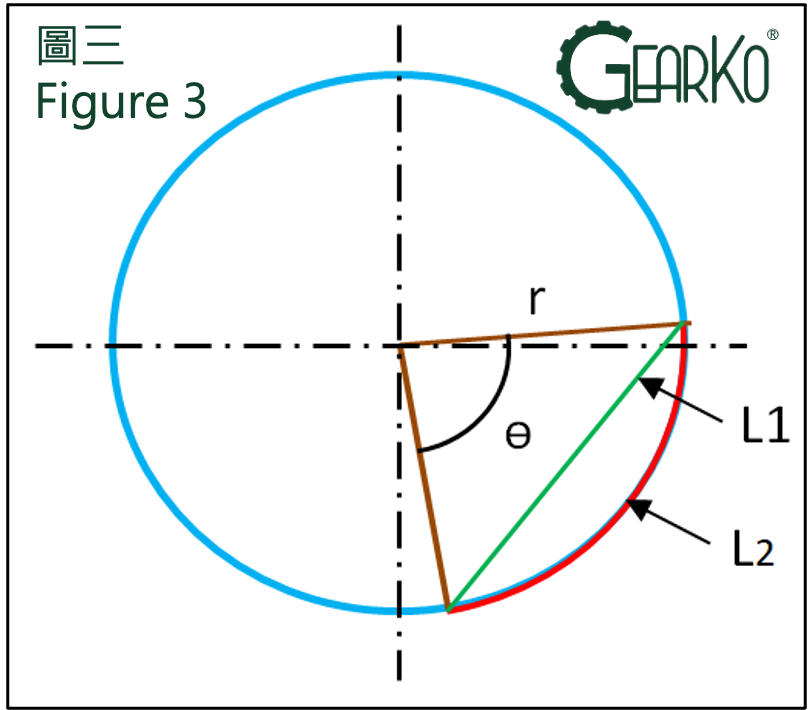
Note 1: The values measured with a dial (or digital) indicator are straight-line distances, which are not equal to the arc length. However, since the angle displacement is very small, the difference between the straight-line and the arc length can be considered negligible under the condition of a 1-degree (60 minutes) angle with a 300mm radius, as shown in Table 1 below.

Therefore, this difference can be ignored, and the measured length value can be directly considered as the arc length for calculations.

 

For a radius of r=300 mm

formula	L1=r*√(2-2cosθ)		L2=2･π･r*(θ/360)		Difference (mm)
No.	Degree θ(°)	straight-lineL1(mm)	Degree θ(°)	arc lengthL2(mm)
1	30	155.2914	30	157.0796	1.7882
2	20	104.1889	20	104.7198	0.5308
3	10	52.2934	10	52.3599	0.0664
4	5	26.1716	5	26.1799	0.0083
5	1	5.2359	1	5.2360	0.0001