齒隙？背隙？回程間隙？弧分？行星減速機精度的關鍵

簡單來說行星式減速機的精度，通常是指由動力源輸入，在傳動過程中，對於最終端執行元件，產生運動的準確性和均等性的影響程度。

以下的探討是以齒輪的影響來說明精度，而實際上減速機的各個相配零件的加工誤差、幾何誤差和組裝品質，也都是會影響減速機精度的重要因素。

 

• 名詞解釋：
  1. 回程間隙j_t [ arcmin ]：名詞
         指減速機輸出軸與輸入端的最大偏差角，測量時先將齒輪輸入端固定住，然後在輸出軸加載一定的扭矩，以克服齒輪箱內的摩擦力和油膜阻力，一般會使用額定扭矩的2~3%扭矩，此時減速機輸出端有一個微小的位移，此角位移即為回程間隙，其單位為「弧分」，即六十分之一度。
  2. 弧分[ arcmin ]：單位量詞(60進位制的角度單位)也可稱”角分”
         因為是60進位制，單位關係如下說明，1°（度）= 60’（角分）= 3600”（角秒）。一個圓有360度，1度可分為60弧分，即一個圓有21600弧分，如回程間隙標為1 arcmin 時，意思是說減速機轉一圈，輸出端的角偏差1/60度。
         在實際應用中，這個角偏差與軸直徑及轉盤大小有關。
     例如：輸出端轉盤半徑為300mm時，齒輪箱精度為jt=3 (arcmin)時，減速機轉一圈的偏差為b=0.26mm。可參考 「二、說明： A.」的計算公式。
  3. 背隙[Backlash]、齒隙[ Face clearance between gear tooth ]：名詞
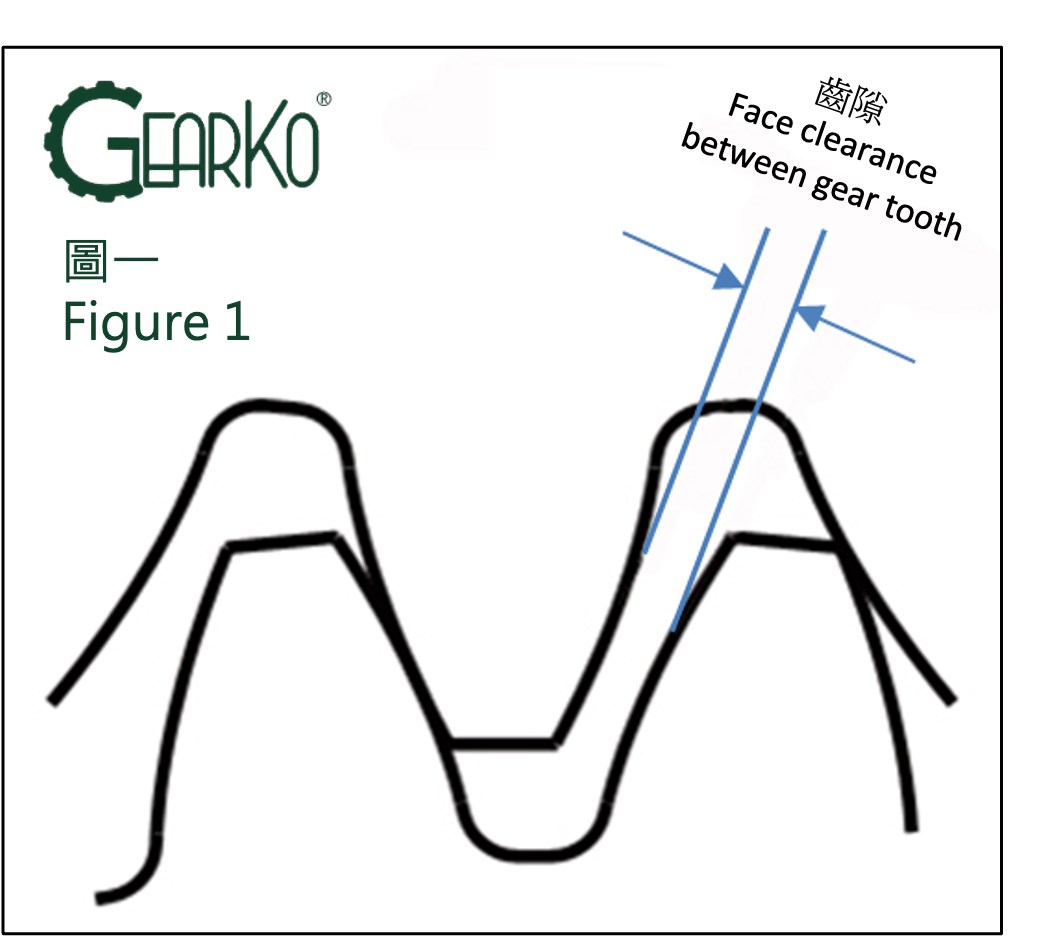
         此處以最直覺的法線方向間隙來討論，是指兩齒輪其中一側的嚙合面接觸時，另一側非嚙合齒面的最短距離，如下圖一所示。
         除了法線方向間隙，還有圓周方向齒隙、回轉角度齒隙、半徑方向齒隙，以上因公差所產生的間隙也會影響整體的精度。

 

• 說明：
  1. 回程間隙(弧分)：
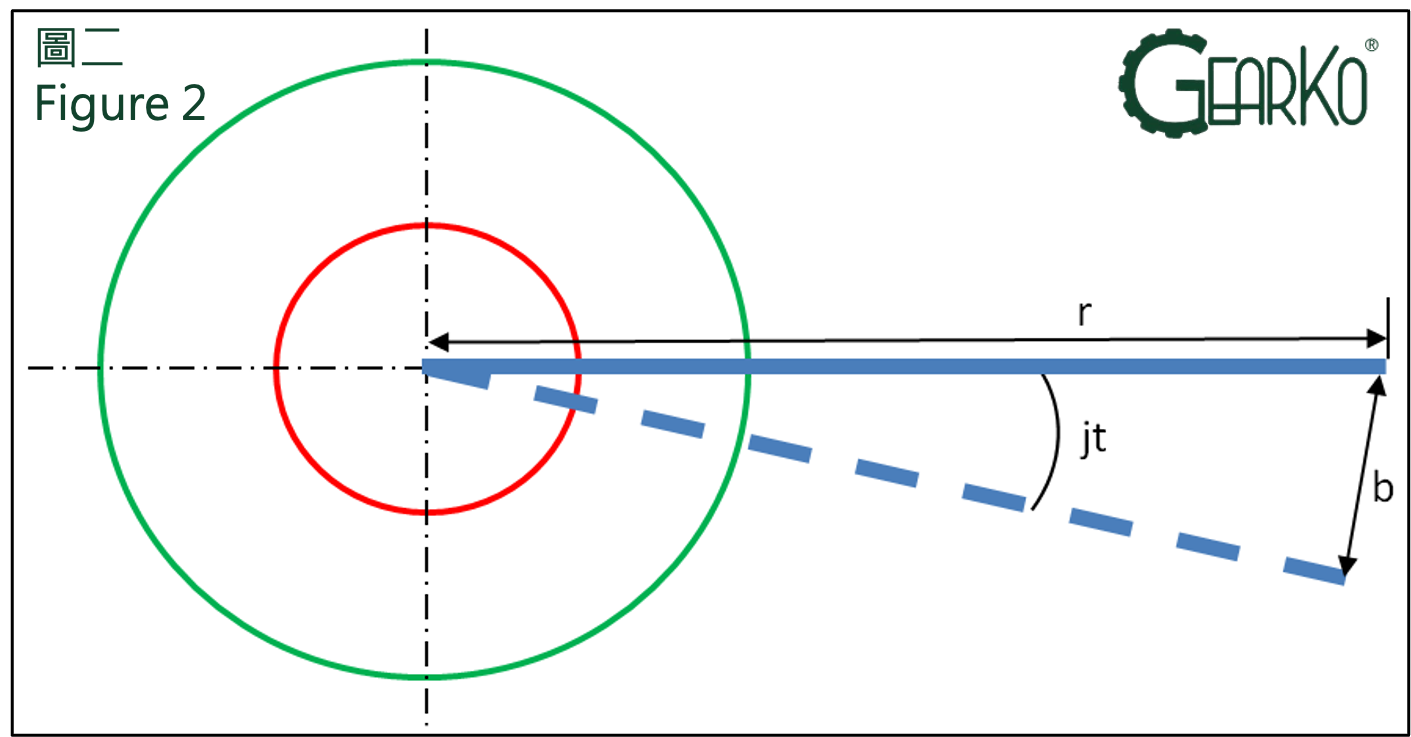
         接下來用手工量測的概念來解釋，回程間隙其實就是用弧長來換算成角度。一般使用手工量測時，先將輸入端固定，再輸出端安裝一個比較長的力臂，用千(百)分錶來測量一定距離的位移量(註1.)，並計算出相對應的轉動角度，也就是回程間隙(弧分)，如下圖二所示。

範例：

弧分公式：jt=bx21600/(2･π･r)，半徑r=300mm，弧長b=0.26

弧分jt=0.26 x21600/(2･π･300)≒3 arcmin

1. B. 背隙、齒隙：

    齒隙的大小，是影響回轉間隙的直接因素，因為齒輪轉動時是齒面與齒面發生滾動加上滑動的運動狀態，如果齒輪與齒輪之間沒有縫隙，則會因干涉過大而無法轉動，所以齒隙是齒輪傳動必要的設計。
    若是只往單一方向運轉，齒輪與齒輪就會保持接觸，齒隙就不會造成問題。但是運動方式為往復運轉時，齒隙就會導致，當馬達完成訊號輸入的動作而停止時，但最終的定位點，因為齒輪反向旋轉時，會先有一小段的齒隙，然後才會碰到齒輪再將動力傳出。
    以微觀的角度來說，因為有一小段的齒隙，造成動力源空轉，如此一來輸入角度會無法完全輸出到最終位置。而齒隙太大精度會降低，齒隙太小又會影響運轉順暢度，因此才會提高行星式減速機加工的困難度與成本。

 

• 應用：
  1. 旋轉運動：
     例如：輸出端轉盤半徑為500mm時，減速機精度為3 arcmin時，
     在圓盤的最外側弧線偏差值為0.44mm。
  2. 直線運動：
     例如：滾珠螺桿導程20mm，減速機精度為3 arcmin時，
     直線偏差值為20/21600*3=0.00278mm。

如上述的兩種應用方式，便可清楚看出減速機精度，在不同的應用方式所造成的偏差，而偏差值是否為可接受的範圍，就需要進一步的了解使用者的需求。

 

• 結論：

當有人詢問齒隙、背隙、回程間隙、弧分是多少時，就好像是有人問：

1. 請問這個啞鈴重量是多少?  請問這個啞鈴幾公斤?

2. 請問這支釣竿長度是多少?  請問這支釣竿幾呎?

其實也只是口語化的說法不同，通常業界人士都能理解是在問什麼?

就是想知道減速機的精度是多少弧分?

 

如同一開始所說，影響行星式減速機精度的因素有許多，在實際測量與理論值一定會有偏差，尤其是多級減速機，因為每一級間隙的影響，以及每個嚙合環節的間隙並不相同，再加上各種不同的誤差，都會影響整體齒輪轉動的精度。

台灣格高GearKo減速機具有極好的精度、剛性和很高的可靠性，性價比不輸任何有品質的品牌。若有需求或問題，也歡迎來電或電子郵件與台灣格高GearKo聯繫。

 

 

 

 

註1.使用千(百)分表量測出來的值，屬於直線距離，與弧長不相等，但因為角位移距離極小，可參考下表一的差異值，在夾角1度(60分)，半徑300mm的條件下，直線與弧長的差異幾乎為0。

故可忽略兩者的差異，直接將此長度數值當成弧長來計算。

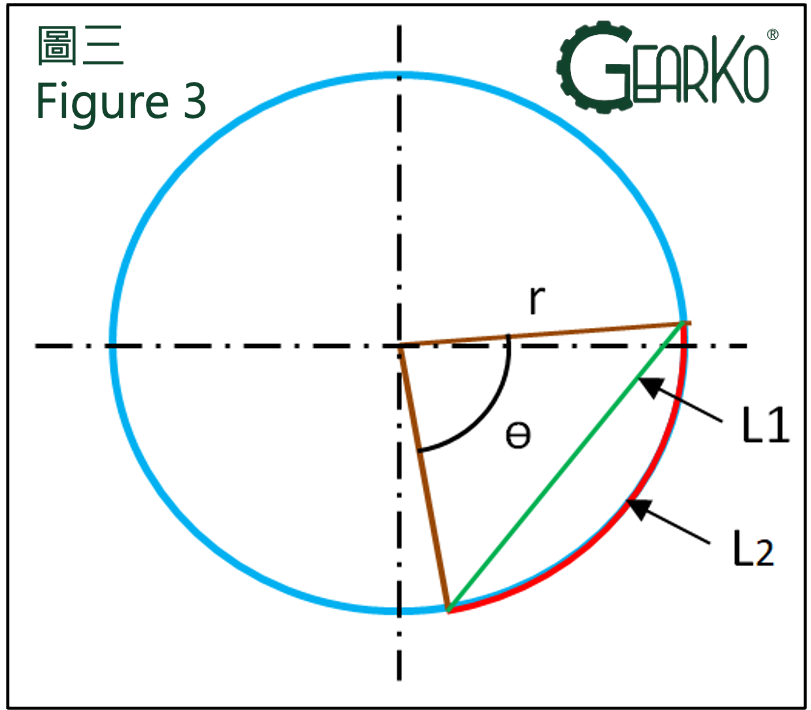
以半徑r=300mm來計算

公式	L1=r*√(2-2cosθ)		L2=2･π･r*(θ/360)		差異值 (mm)
編號	角度θ(度)	直線L1(mm)	角度θ(度)	弧長L2(mm)
1	30	155.2914	30	157.0796	1.7882
2	20	104.1889	20	104.7198	0.5308
3	10	52.2934	10	52.3599	0.0664
4	5	26.1716	5	26.1799	0.0083
5	1	5.2359	1	5.2360	0.0001

表一、